Tenslotte als nabrander en om het af te leren een (halfslachtige …) poging om de onverklaarde grootheden in het model van Piketty van een theoretisch fundament te voorzien. Piketty had als onverklaarde grootheden: de groeivoet van de economie (g), de spaarquote (s) en de vergoeding op kapitaal (r).
Als op termijn het aandeel van kapitaal in het totaal verdiende inkomen erg groot wordt (met daarbij een hoog vermogen en hoge voorraad kapitaal) dan lijkt het minder waarschijnlijk dat de rentevoet hoog blijft (afnemende opbrengsten van kapitaal als de voorraad groter en groter wordt, uitputting van innovatieve mogelijkheden). Ik heb daarom een eigen modelletje gemaakt die deze variabelen wel opneemt zonder daarbij al te veel van het originele modelletje van Piketty af te wijken.
Het model van Piketty luidt (herhaling uit vorige blog):

Aanpassing aan model Piketty
Ik introduceer een productiefunctie die weergeeft dat je met een bepaalde hoeveelheid arbeid en een hoeveelheid kapitaal maximaal Y goederen kan produceren. Ik veronderstel niet meer dat het inkomen elk jaar toeneemt met een vast percentage maar verander dat in: elk jaar wordt arbeid en kapitaal iets productiever zodat er elk jaar iets meer goederen kunnen worden geproduceerd (bij gelijkblijvende hoeveelheden arbeid en kapitaal). Dus exogene groei wordt veranderd in (exogene) technologische ontwikkeling RHO. De hoeveelheid werk noem ik L (van labour).
Y = f(L, CAP)
Ik neem aan dat het arbeidsinkomen LI is opgebouwd uit de hoeveelheid uren/werk (werkgelegenheid L) x het uurloon (w).
LI = L . w
Om bij dezelfde getallen als Piketty te blijven, kom ik bij de gekozen parameters voor de (CES-) productiefunctie uit op 1.500 uur per jaar x een uurloon van € 14, maakt tesamen een arbeidsinkomen van € 21.000 / jaar. De productie neemt, zoals hiervoor gesteld, jaarlijks toe met de groei in de techniek door innovatie met een percentage RHO%. Ik neem aan dat de hoeveelheid arbeid gelijk blijft (L is constant, je week wordt immers niet steeds langer) en dat de lonen mee-stijgen met de (arbeids-)productiviteit.
Het verdiende inkomen blijft daarmee per definitie NI = LI + CI.
Het kapitaalsinkomen blijft hetzelfde als hiervoor, namelijk de rentevoet maal de hoeveelheid kapitaal. Maar de rentevoet is in mijn model niet meer constant en vast. Ik ga ervan uit dat de rente zodanig aanpast dat de vraag naar goederen gelijk wordt aan de totale maximale productiecapaciteit, oftewel:
Y = NI (via aanpassing van de rente)
Natuurlijk blijft per definitie gelden dat de nieuwe hoeveelheid kapitaal gelijk is aan de oude hoeveelheid kapitaal plus de toevoeging in de vorm van besparingen. Maar de besparingen bij Piketty gingen uit van een vast spaarpercentage s van het inkomen. Het klinkt logischer om het sparen afhankelijk te laten zijn van de hoogte van de rente. Hoe hoger de rente hoe meer er gespaard gaat worden. Ik gebruik hiervoor de relatie:
s = s(-1) . r(-1)/r
Met andere woorden: als de rente omlaag is gegaan in de vorige periode dan betekent dat dat ik nu in deze periode minder ga sparen en dus meer zal consumeren. En omgekeerd natuurlijk: een hogere rente lokt uit tot meer sparen.
Het totale nieuwe modelletje ziet er nu als volgt uit:
(1) Y = f(L, CAP) *
(2) NI = LI + CI
(3) LI = w . L
(4) w = w(-1) . (1+RHO)
(5) CI = r . CAP
(6) R | Y = NI (rente volgt uit gelijkstelling van Y aan NI, van productie aan inkomen)
(7) CAP = CAP(-1) + SAV
(8) SAV = s . NI
(9) s = s(-1) . r(-1)/r
Simulatie
Werken met de spreadsheet gaat overigens niet meer (zo makkelijk) omdat er sprake is van een aantal simultane vergelijkingen.
De uitgangssituatie is zodanig gekozen dat er geen verschil is te zien met Piketty:
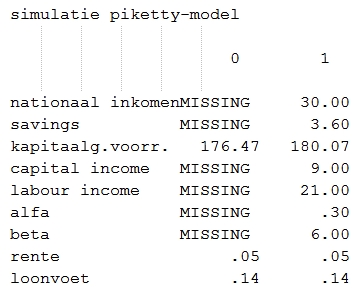
Inkomen is weer 30.000 Euro/jaar met een verdeling over arbeid (€ 21.000) en kapitaal (€ 9.000). De loonvoet is € 14 / uur bij een werkgelegenheid/baan van gemiddeld 1.500 uur, de rentevoet 5% bij een kapitaalhoeveelheid van € 180.000. De simulatie bij een technologische vooruitgang voor arbeid én kapitaal van 2% (komt overeen met de groei g van 2% bij Piketty) leidt tot een exact replica van Piketty’s model uit blog 3 van deze serie. Dus de rente blijft mooi constant op 5% en het aandeel van kapitaal blijft 30% bij een kapitaalvoorraad die jaarlijks groeit dankzij besparingen met een s van 12% van het inkomen.
Ook alle volgende perioden zien er exact zo uit als bij Piketty. Bij Piketty groeide het inkomen autonoom met 2% per jaar, bij mij is dat ingesloten via de stijging van de innovatiekracht met 2% per jaar (en daarmee een stijging van de loonvoet).
Nulgroei?
Kortom: een uitgebreider model dat ook verklaart waar de groei, de rente en de besparingen vandaan komen en wat dezelfde cijfers laat zien. Dus … niets opgeschoten. Niet helemaal waar. Het gaat er nu om dat als de groei achterblijft te kijken wat er dan gebeurt. Bij Piketty had ik in blog 3 laten zien dat bij een nulgroei van de economie in periode 20 het aandeel kapitaal in het totale inkomen al was toegenomen van 30% naar 40%.
Nu is het interessant te kijken wat er gebeurt als ik in het uitgebreidere model ook van nulgroei uitga. Dus geen enkele technologische ontwikkeling meer maar toch moet elk jaar rente worden verdiend op de voorraad kapitaal. Zal ook nu het arbeidsinkomen worden verdrongen door het opslurpende effect van de rente op kapitaal?
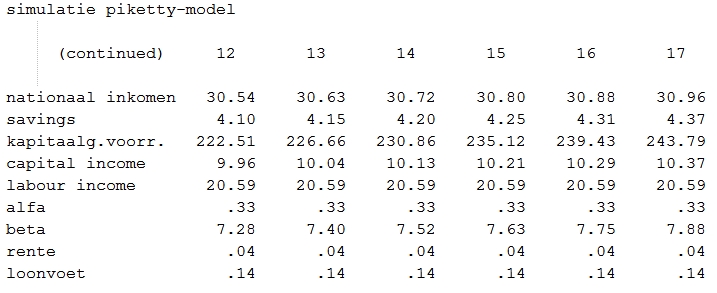
We zien dat het nationaal inkomen ook in mijn geval gelijk blijft op ongeveer € 30.000. Terecht want er is geen ontwikkeling meer in techniek. Ook de loonvoet blijft dus gelijk op de € 14 per uur van de startsituatie, ook logisch. In de tabel hierboven zie je nog iets andere waarden voor het inkomen in perioden 12-17 maar dan zijn afrondingsverschillen uit de berekeningen. Ook het looninkomen blijft nu dus in de tijd gelijk. Maar dan krijgen we een simpel iets: lonen kunnen niet meer worden verdrongen, en dus moet het aandeel kapitaal ook gelijk blijven. En aangezien de voorraad kapitaal wel degelijk blijft stijgen (door de besparingen) kan het niet anders of de vergoeding op kapitaal moet zakken. En dat is wat we ook zien terug komen in de simulatie. De rentevoet zakt van 5% naar 4% (dat lijkt niet veel maar dat is een daling van 20%).
Conclusie
We kunnen makkelijk zat een modelletje maken dat laat zien dat het aandeel van kapitaal helemaal niet toeneemt als de groei stagneert. Integendeel juist: de kapitaaleigenaren zitten in hun eigen cirkel gevangen, een steeds hogere voorraad kapitaal leidt tot een alsmaar dalende vergoeding of rente. Dat klinkt mij ook logisch in de oren: een steeds grotere voorraad vermogen die naar een niet bestaande aanwending zoekt kan alleen maar resulteren in een dalende rente.
En toch is dat niet wat we zien. Die rente blijft ook bij een lagere groei rond die 5% hangen. Dat is wat Piketty uit de historische cijfers laat zien. Maar niet echt verklaart. Dus wat is de onderliggende onderbouwing/theorie achter de cijfers van de laatste 300 jaar?
Toch weinig opgeschoten, ik geef het toe. Heeft me meer tijd gekost dan me lief is. THE END wat mij betreft van Piketty voorlopig.
Rudy van Stratum
Noot *: De productiefunctie (1) is een zogenaamde CES-functie die is gecalibreerd op de getallen van Piketty. Hierbij is sprake van een ‘voorvermenigvuldigfactor’ die een indicatie is van de stand van de techniek. De aanname is dat elk jaar deze voorvermenigvuldigfactor autonoom groeit met een percentage g. Dus met eenzelfde hoeveelheid arbeid en kapitaal kun je dan elk jaar g% meer goederen produceren. Dat komt dan effectief op hetzelfde neer als de aanname van Piketty dat het inkomen/productie elk jaar met g% groeit met dat verschil dat ik dat nu terug kan herleiden naar de inzet van arbeid en kapitaal.

Bedankt voor deze 6 bijdragen. De kennis van deze dummy over Piketty (en de economie) is weer gegroeid.
Gegeven jou conclusie: toch geen Nobelprijs voor de economie voor Piketty?
Rudy, dank voor de berekeningen en de verhelderende toelichting. Ik denk dat Piketty scheef zit met z’n cijfers, hij meet wellicht de economische groei verkeerd, groei is er immers ook als het BNP niet toeneemt. Een beter product voor hetzelfde geld is immers ook economische groei (alleen moeilijk meetbaar). Wellicht ook dat het rendement op kapitaal niet volledig geïnvesteerd wordt in de voorraad kapitaal, waardoor de groei achterblijft. In dat geval is weliswaar r > g, maar groeit het vermogen niet per se harder dan de economie.
Overigens zou je ons ook eens moeten uitleggen hoe de inkomens kunnen groeien als er geen inflatie is. Meer producten bij een gelijkblijvende geldhoeveelheid geeft lagere stuksprijzen, geen hoger inkomen.
In principe kijk je bij (echte) groei niet naar nominale grootheden maar corrigeer je voor inflatie. Het inkomen neemt dan dus toe vanwege hogere aantallen geproduceerde goederen. Gaat te ver dat hier uit te werken maar gaat zover ik kan zien in genoemde cijfervoorbeelden wel goed.
Oke, maar hoe wordt die inflatie gemeten? De officiële inflatie-cijfers geven allang de werkelijkheid niet meer weer. Als de inflatie echt op 2% was gehouden, dan hadden we geen vastgoedbubbel gehad en dus ook geen kredietcrisis. Ik denk dat als we naar de werkelijke economische groei kijken, dus gecorrigeerd met reële inflatie-cijfers, er een veel hogere groei is. Weliswaar niet in puur inkomen, maar wel in de hoeveelheid geproduceerde goederen en diensten.
Om terug te komen op het hogere inkomen, als er meer goederen geproduceerd worden bij een gelijkblijvende geldhoeveelheid, dan dalen simpelweg de stuksprijzen. Niks mis mee, want de welvaart is wel toegenomen, er zijn immers meer producten. Helaas wordt dit vaak uitgelegd als deflatie, maar dat is het feitelijk gezien niet, de geldhoeveelheid blijft immers constant.
Overigens ben ik ook wel benieuwd hoe de cijfers er uit zien als blijkt dat een groot deel van het kapitaal geïnvesteerd is in staatsobligaties in plaats van productie-capaciteit. Staatsschulden kunnen best zinvol zijn, maar of het nou echt welvaart genereert? Zou maar zo kunnen dat we hier de oorzaak van r > g gevonden hebben. Ik denk dat de economische groei sterk verbetert als een groter deel van de besparingen in productie-kapitaal geïnvesteerd wordt in plaats van uitgegeven door de overheid.
Zou de rente op vermogen misschien 5% blijven, omdat het kapitaal niet in eigen land wordt geïnvesteerd, maar steeds ergens anders ?
Het houd dan op als er niet meer ergens anders is.
Dat zou ook verklaren waarom in 1945-1970 een andere situatie ontstond, omdat het ineens rendabeler was om kapitaal in eigen land te investeren ?
Dat is zeker een belangrijke verklaring. Kapitaal zoekt voortdurend naar het hoogste rendement en de globalisering (internet, opkomst China etc) maakt het mogelijk alsnog die 5% te halen. En als dat zo is: zou dan ná het afromen van die kansen én bij het uitblijven van nieuwe technieken etc de voorspelling van Piketty van 4-5% ophoudente bestaan?
En nog even een herhaling van mijn eigen ongelijkheidsberekening:
. In 17e eeuw waren meeste rijksten, die wij behandelen, guldenmiljonairs, dat 3.333x jaarinkomen (300) ambachtsman was. In heden hebben we van doen met euromiljardairs, dat 47.619 x jaarinkomen (21.000) ambachtsman is. Mogelijke verklaring is dat er destijds grens zat aan graaien, omdat anders de burgers zouden sterven en er niks te verdienen viel. Tegenwoordig ligt de ondergrens van inkomen veel hoger, dus valt er meer te graaien. Het was dus een slimme zet van liberalen om de welvaart van bevolking te verhogen, waardoor je zelf nog veel meer kon cashen (VGL Galbrath). Overigens kon dat ook alleen door bevolkingsgroei/concentratie en massaproductie.
Bovendien zien we bij de cijfers van Maddison dat de ongelijkheid geglobaliseerd is. We kunnen meer graaien uit de rest van de wereld!! In 1600 2x en in 2000 18x)( Tot 1600 was het verschil in rijkdom (gdp/cap) tussen de rijke regio’s en de rest van de wereld altijd ongeveer 2x. Vanaf 1600 gaat dat verschil stijgen naar 5x (1700), 4x (1820), 8x (1900), 18x (2000).)
!!De 20 miljonairs uit 250 rijksten Gouden eeuw hadden gezamenlijk 55,9 miljoen en dat is 1,4% van GDP (Madisson in 1700 ongeveer 4.000 miljoen); de 20 miljardairs uit heden hebben gezamenlijk 57,9 miljard (2007) en dat is 14% van GDP (400 miljard = 100xh). In heden in NL dus 10 x zo rijk ! Men zou dat niet verwachten, maar dat is heden dus veeeeel meer.
(De 20 rijksten van nu (2007) 57,9 miljard euro en de 20 rijksten van gemiddeld 1650 omgerekend voor inflatie 559 miljoen euro = 103 x meer. Jan modaal GDP/C (volgens Madisson) 1.750 in 1650 en heden 23.388 Gary-Khamis dollars = 13 x meer SLECHTS.)
Die stijgingen in verschillen lopen ongeveer parallel met laatste decennia. Overigens kom je hiermee op zo’n 4% stijging per jaar voor Jan Modaal en zo’n 30% voor de rijksten (klopt dit allemaal zo’n beetje ??? Rudy).
Het optimum lijkt dus dat Jan Modaal in ieder geval vooruit gaat, maar dat hoeft maar minimaal te zijn.
– Verders heeft CBS statistiek in jaren negentig veranderd naar huishoudens. De hogere inkomens/vermogens van Jan Modaal zou wel eens grotendeels te verklaren zijn uit werkende vrouwen. Per uur arbeid is inkomen/vermogen dan helemaal niet gestegen.
– Groei ongelijkheid en groei laagste inkomens is wel afhankelijk van economische groei en die is sterk afhankelijk van energiebronnen en vervuiling. Dat is momenteel een heikele kwestie.
Jos, ik denk dat gemiddeld 5% rendement op geïnvesteerd kapitaal een soort van natuurlijk evenwicht is, stijgt het rendement boven de 5%, dan trekt het extra besparingen aan, waardoor er overcapaciteit ontstaat en het rendement vanzelf daalt. Andersom, als het rendement onder de 4% daalt, dan wordt er minder geïnvesteerd, productie-capaciteit loopt terug, er ontstaat schaarste waardoor de winsten toenemen en het rendement stijgt.
Daarnaast, als de productie-capaciteit (het kapitaal) met 5% groeit, dan zal ook de output met 5% toenemen (de economie groeit dan met 5%). In de praktijk gebeurt dat echter niet altijd, waarschijnlijk omdat niet alle besparingen geïnvesteerd worden in productie-capaciteit, maar uitgeleend aan overheden. Kapitaal in de vorm van staatsschuld rendeert wel, maar de economie groeit er niet van.
Een oplossing van de groeiende vermogensongelijkheid is dus niet het confisceren van vermogen, maar het terugdringen van de overheidsschulden.
Beste Henry,
IK heb van mijn leermeester (Brenner, ontwikkelingseconomie) geleerd dat de zon op aarde een rendement heeft van ongeveer 5%. Hogere rendementen behalen we alleen door roofbouw. Maar die 5% is een gemiddelde en de elite behaalt mi hogere rendementen en het volk lagere.
Overigens heb ik van een andere leermeester astronoom geleerd dat er nog andere energiebronnen uit het heelal op de aarde neerdalen, waar we niks mee doen. Maar dat terzijde.
Uit mijn onderzoek naar elites door de eeuwen heen, blijkt dat ze het grote geld verdienen met speculatieve en boevige activiteiten, die de samenleving niet veel welvaart brengen. Daarna gaat het al snel in veilger havens: 1/3 staatsleningen, 1/3 OG en 1/3 aandelen.
Staatsleningen zouden economische groei kunnen veroorzaken als de staat goed investeert. Daar komt nog bij dat merkwaardig genoeg uitgaven in zorg niet als economische groei/ consumptie worden gezien. Het is dus ook een kwestie van definitie.
Dat brengt ons op een ander punt dat superrijkdom geen probleem zou zijn als die vermogens maar voor de samenleving goed geïnvesteerd zouden worden.
Beste Rudy,
Maar het draait wel om omzetten op de beurs, als je de aarde van de koers wil bepalen. Zou hier eigenlijk voor gecorrigeerd moeten worden ?
Hetzelfde kun je zeggen van de rendementen op kapitaal. Tot 1900 was er een tekort op kapitaal. Zou de grotere invloed van de staat cq Centrale Bank een rol spelen bij verruiming (geld scheppen) van de kapitaalmarkt vanaf ongeveer 1900, waardoor er meer kapitaal beschikbaar komt met dalende rendementen tot gevolg ?
Heb jij Piketty trouwens helemaal gelezen ?
Komt bij dat de formele rendementen op kapitaal voor 1900 niet zo heel veel zegt. In mijn onderzoek bleek dat die superrijken een deel van hun leningen nooit terug kregen of maar voor de helft, waardoor de rendementen niet waren wat het leek. OG was beter, maar hield ook op bij 4%.
Verder zou de daling van rendement op kapitaal in 20e eeuw kunnen komen door opkomst van graaiende staat, zoals vorsten in middeleeuwen.
De daling van rendement op arbeid wordt mogelijk door Heleen Mees terecht toegewezen aan overaanbod door BRIC en O. Europa vanaf 1980.
Verder denk ik dat uiteenlopen vooral komt door automatisering, waarvan rendement vooral terecht komt bij investeerders, factor kapitaal.
Bovendien viel me op in de grafieken dat rendement op kapitaal en arbeid eigenlijk tot heden aardig in de pas lopen. Is die uiteenlopende extrapolatie wel zo OK ? Veel overgeerft kapitaal verdwijnt gewoon binnen 1 generatie.
Hoor graag van je.
Groetjes, Jos
Natuurlijk heb ik het helemaal gelezen …